Oftentimes in a problem-based curriculum like ours, teachers wonder, "When am I allowed to . . . say . . . things? To explain about math?"
One answer comes from a 1998 study in which Schwartz and Bransford asked a group of students to look at images similar to this one and come up with their own measure for mean absolute deviation.
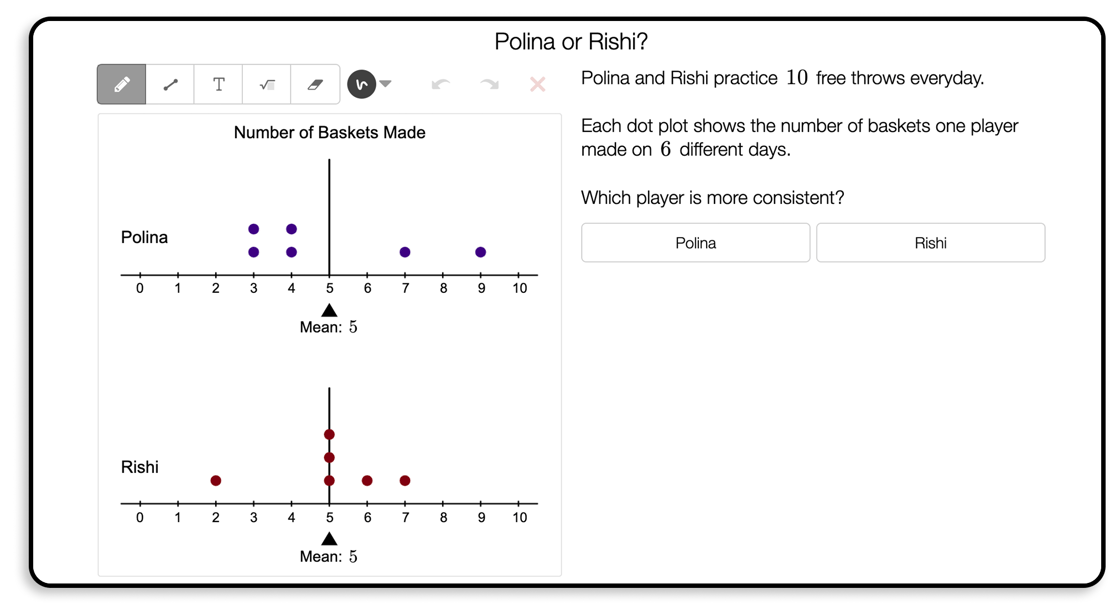
The students in that study struggled for a time that was brief but meaningful. None of them devised the formula for MAD on their own. Later, Schwartz explained the formula.
In another group of students, Schwartz explained the formula right away and asked students to practice using it. Both groups spent similar time working on MAD, but their work was different. On two subsequent tests, including one that was weeks later, students in the first group demonstrated greater learning gains than students in the second group.
I hope this study offers an insight into the work of teaching—yours and ours.
Our work is to offer students experiences that encourage them to start with their senses, to wonder, "Who seems more consistent between Polina and Rishi? What are my senses telling me?"
Your work then is to offer an explanation that is timely and rich. Timely, in that it takes place after students have had a chance to orient their senses to the math. And rich in that it draws on the sensory observations they offer you.
Your knowledge of math and teaching is an invaluable resource to your students. We'd never want you to hide it. We just want to help you find the right time and place to offer it.
Dan & the Desmos Classroom Team
PS. Please give us feedback on the last lesson.
Use the feedback form or just click your answer below then click "Submit" on the form!
How likely is it that you would recommend this lesson to a friend or colleague?
Previous Previews
.png?width=1200&height=120&upscale=true&name=DM_Logo_6-A1%20(1).png "DM_Logo_6-A1 (1)"){kind=logo}